In this post, we introduce GANSynth, a method for generating high-fidelity audio with Generative Adversarial Networks (GANs).
 Colab Notebook Colab Notebook |
🎵Audio Examples | 📝ICLR 2019 Paper |  GitHub Code GitHub Code |
Why generate audio with GANs?
GANs are a state-of-the-art method for generating high-quality images. However, researchers have struggled to apply them to more sequential data such as audio and music, where autoregressive (AR) models such as WaveNets and Transformers dominate by predicting a single sample at a time. While this aspect of AR models contributes to their success, it also means that sampling is painfully serial and slow, and techniques such as distillation or specialized kernels are required for real-time generation.
Rather than generate audio sequentially, GANSynth generates an entire sequence in parallel, synthesizing audio significantly faster than real-time on a modern GPU and ~50,000 times faster than a standard WaveNet. Unlike the WaveNet autoencoders from the original paper that used a time-distributed latent code, GANSynth generates the entire audio clip from a single latent vector, allowing for easier disentanglement of global features such as pitch and timbre. Using the NSynth dataset of musical instrument notes, we can independently control pitch and timbre. You can hear this in the samples below, where we first hold the timbre constant, and then interpolate the timbre over the course of the piece:
| Consistent Timbre |
| Interpolation |
| Bach's Prelude Suite No. 1 in G major (MIDI). Try it yourself with the Colab Notebook. |
How does it work?
GANSynth uses a Progressive GAN architecture to incrementally upsample with convolution from a single vector to the full sound. Similar to previous work we found it difficult to directly generate coherent waveforms because upsampling convolution struggles with phase alignment for highly periodic signals. Consider the figure below:

The red-yellow curve is a periodic signal with a black dot at the beginning of the wave each cycle. If we try to model this signal by chopping it into periodic frames (black dotted line), as is done for both upsampling convolutions in GANs and short-time fourier transforms (STFT), the distance between the beginning of the frame (dotted line) and the beginning of the wave (dot) changes over time (black solid line). For a strided convolution, this means the convolution needs to learn all the phase permutations for a given filter, which is very inefficient. This difference (black line) is called the phase and it precesses over time because the wave and frames have different periodicities.1

As you can see in the example above, phase is a circular quantity (yellow bars, mod 2π), but if we unwrap it (orange bars), it decreases by a constant amount each frame (red bars). We call this the instantaneous frequency (IF) because the definition of frequency is the change in phase in time. An STFT compares a frame of signal to many different frequencies, which leads to the speckled phase patterns as in the image below. In contrast, when we extract the instantaneous frequencies, we see bold consistent lines reflecting the coherent periodicity of the underlying sound.
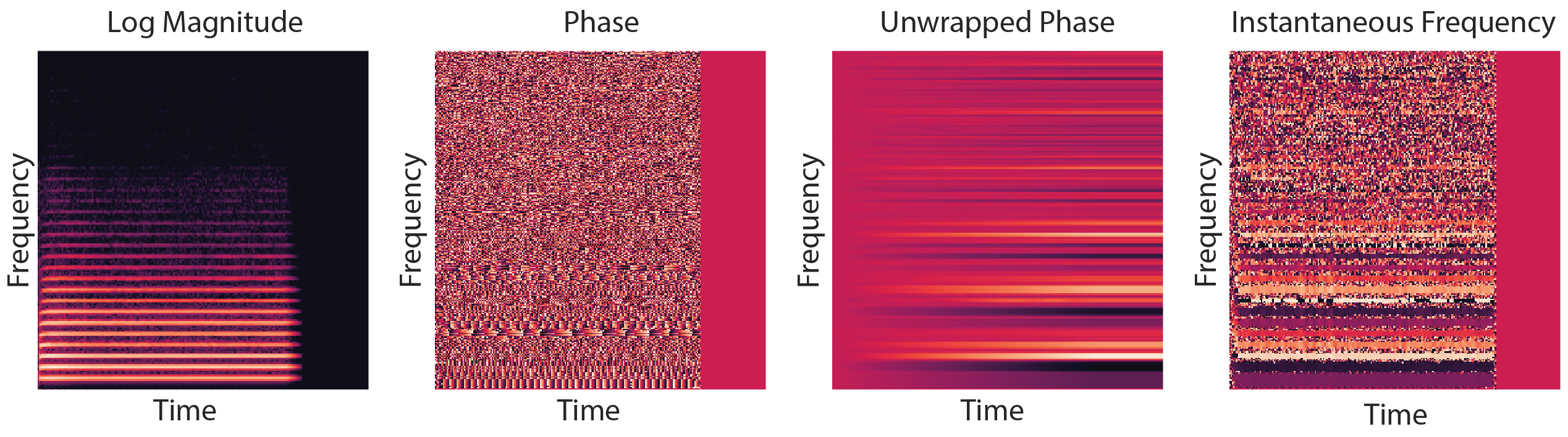
Results
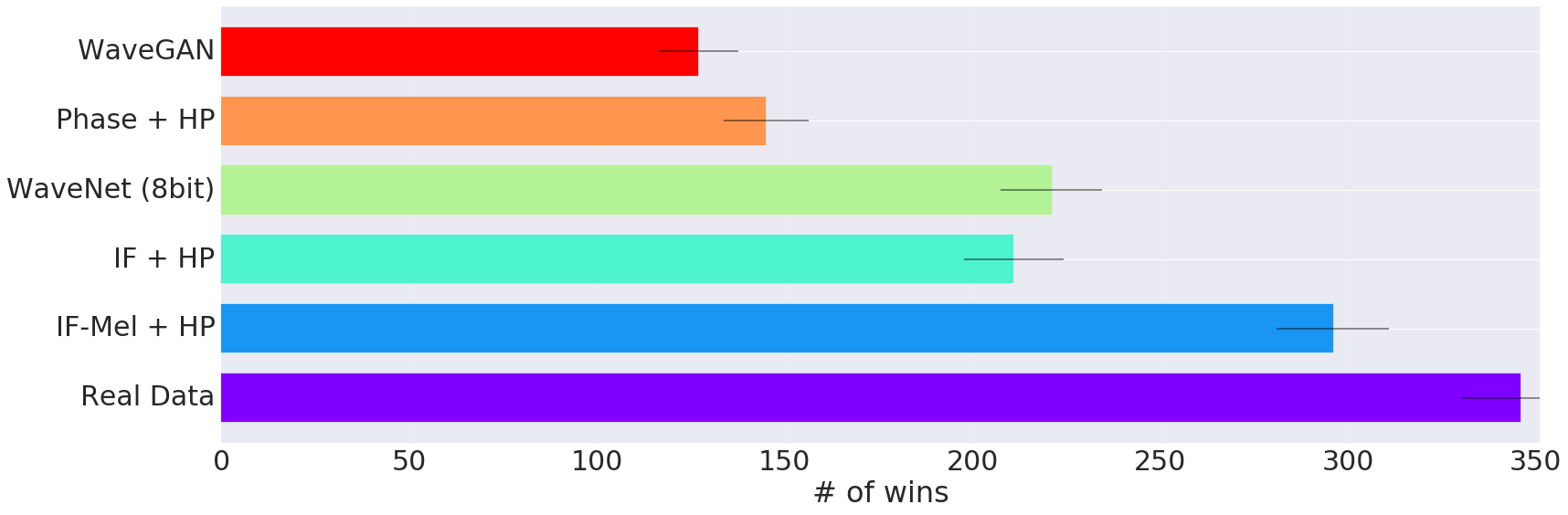
In the GANSynth ICLR Paper, we train GANs on a range of spectral representations and find that for highly periodic sounds, like those found in music, GANs that generate instantaneous frequency (IF) for the phase component outperform other representations and strong baselines, including GANs that generate waveforms and unconditional WaveNets. We also find that progressive training (P) and increasing the frequency resolution of the STFT (H) boosts performance by helping to separate closely-spaced harmonics. The graph below shows the results of user listening tests, where users were played audio examples from two different methods and asked which of the two they preferred:
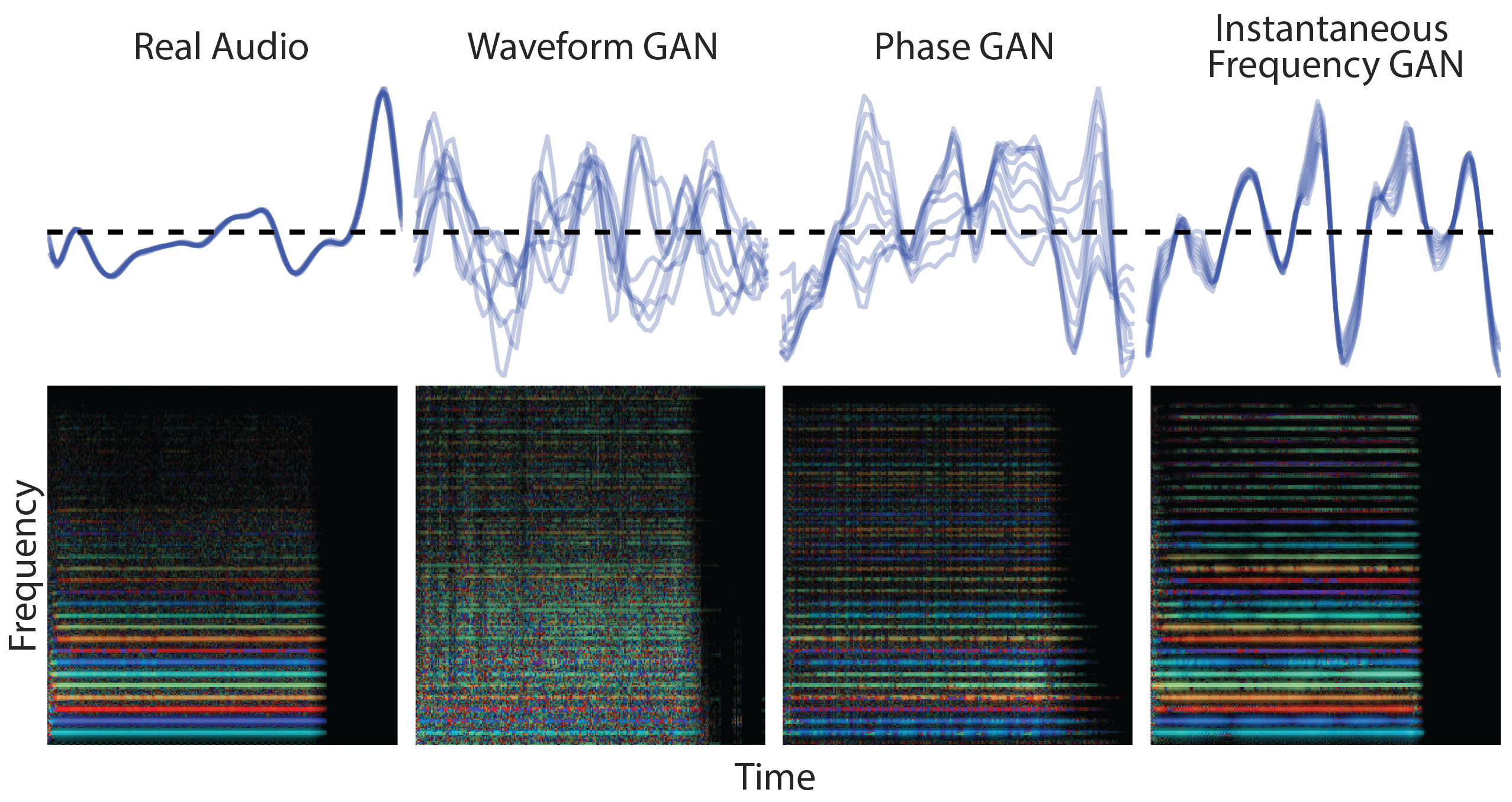
Beyond the many quantitative measures in the paper, we also can see qualitatively that the GANs that generate instantaneous frequencies (IF-GANs) also produce much more coherent waveforms. The top row of the figure below shows the generated waveform modulo the fundamental periodicity of a note. Notice that the real data completely overlaps itself as the waveform is extremely periodic. The WaveGAN and PhaseGAN, however, have many phase irregularities, creating a blurry web of lines. The IF-GAN is much more coherent, having only small variations from cycle-to-cycle. In the Rainbowgrams (CQTs with color representing instantaneous frequency) below, the real data and IF models have coherent waveforms that result in strong consistent colors for each harmonic, while the PhaseGAN has many speckles due to phase discontinuities, and the WaveGAN model is very irregular.
What’s next?
This work represents an initial foray into using GANs to generate high-fidelity audio, but many interesting questions remain. While the methods above worked well for musical signals, they still produced some noticeable artifacts for speech synthesis. Some recent related work builds on this by exploring new methods for recovering the phase from generated spectrograms with fewer artifacts. Other promising directions include using multi-scale GAN conditioning, handling variable length outputs, and perhaps replacing upsampling convolution generators with flexible differentiable synthesizers.
How to cite
If you extend or use this work, please cite the paper where it was introduced:
@inproceedings{gansynth,
title = {GANSynth: Adversarial Neural Audio Synthesis},
author = {Jesse Engel and Kumar Krishna Agrawal and Shuo Chen and Ishaan Gulrajani and Chris Donahue and Adam Roberts},
year = {2019},
URL = {https://openreview.net/pdf?id=H1xQVn09FX}
}
-
Fun fact, this “beating” is a fundamental physical phenomena that gives rise to things as diverse as moiré patterns, aliasing in signal processing, polyrhythms and harmony, and the energy band structure of crystalline solids. ↩
